堆(heap)排序
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆是逻辑上讲是一个完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大根堆;每个结点的值都小于或等于其左右孩子结点的值,称为小根堆。
大根堆结构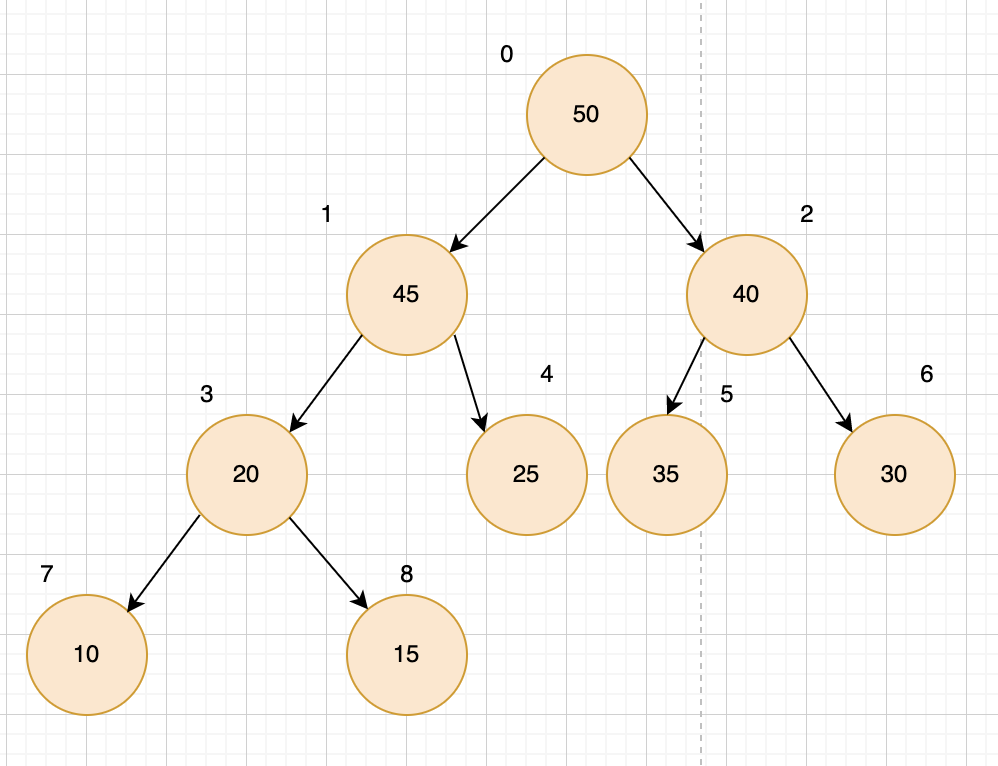
大根堆结构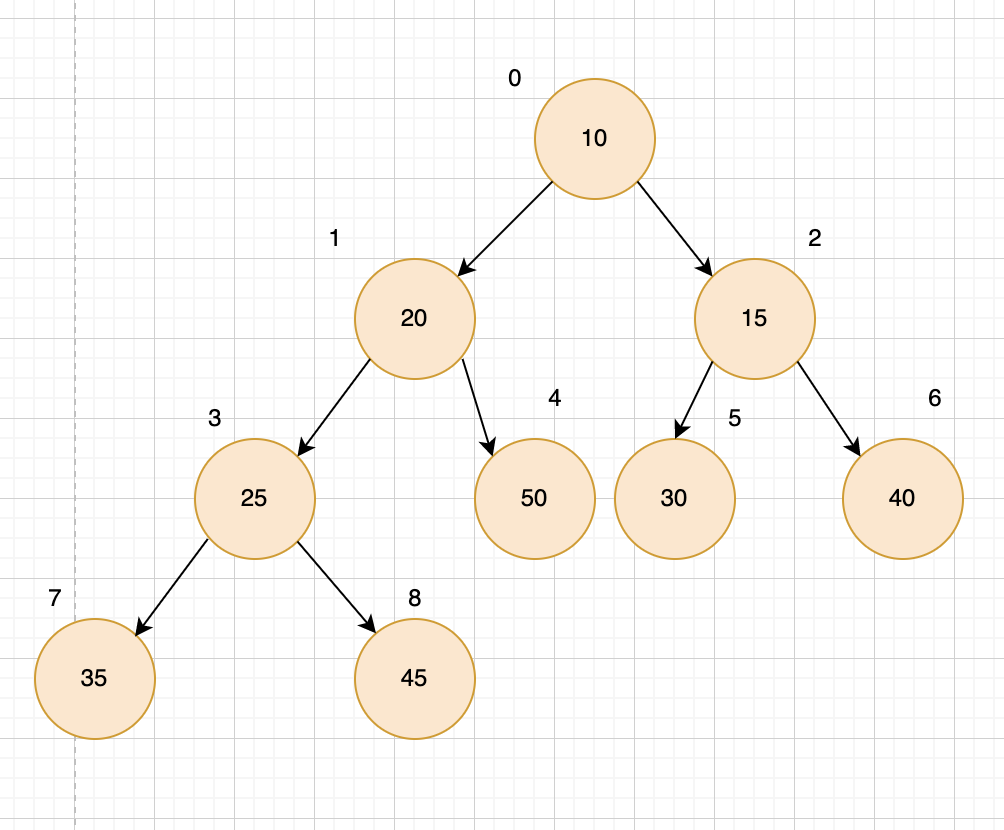
我们对堆中的结点按层进行编号,映射到数组中就是下面这个样子:
节点索引:
- 父节点: (i-1) / 2
- 左孩子节点: i * 2 + 1
- 右孩子节点: i * 2 + 2
堆中父子节点关系:
- 大根堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
- 小根堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
组成堆的节点数大小成为堆大小,heapSize。
堆排序基本思想及步骤
堆排序的基本思想是:将待排序序列构造成一个大根堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
假设下面数字,如何进行堆化?
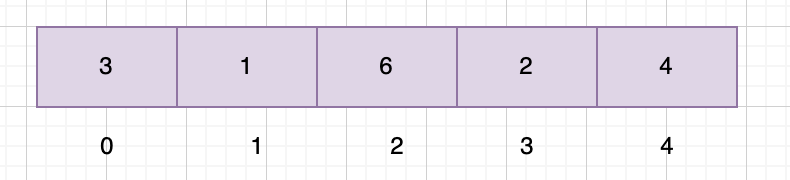
- 首先第一个数字3,即已经堆化。此时heapSize=1;
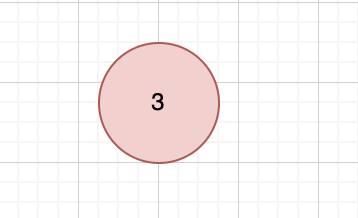
- 第二个数字为1,与父节点比较,小于父节点3,即为左节点。此时heapSize=2;如
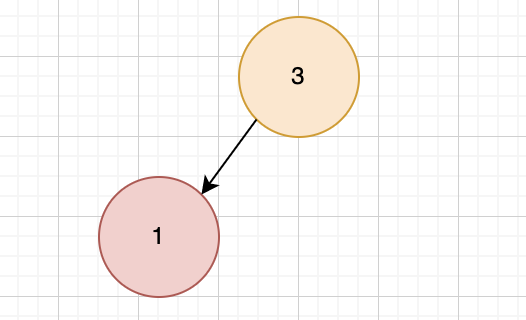
- 第三个数字6,与父节点比较, 6 > 3,则与父节点交换,堆化,此时heapSize=3;
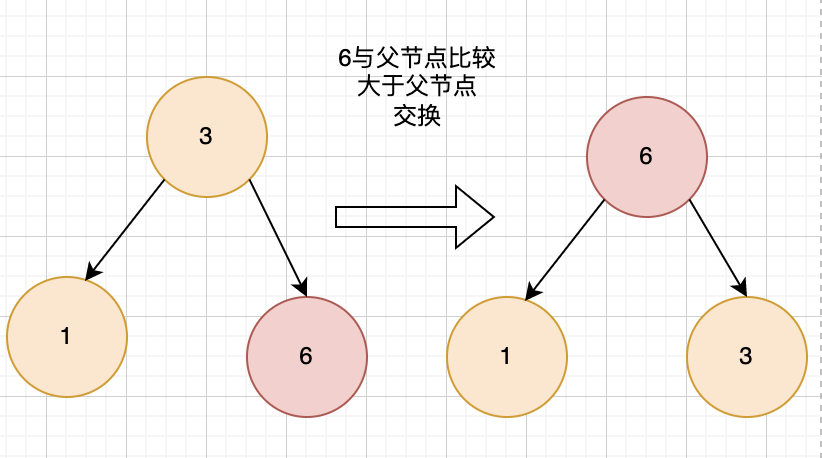
- 第四个数字2,与父节点1比较, 2 > 1,则与父节点交换,此时,2 来到原来1的位置,2继续与父节点6比较,不大于6,暂停,堆化,此时heapSize=4;
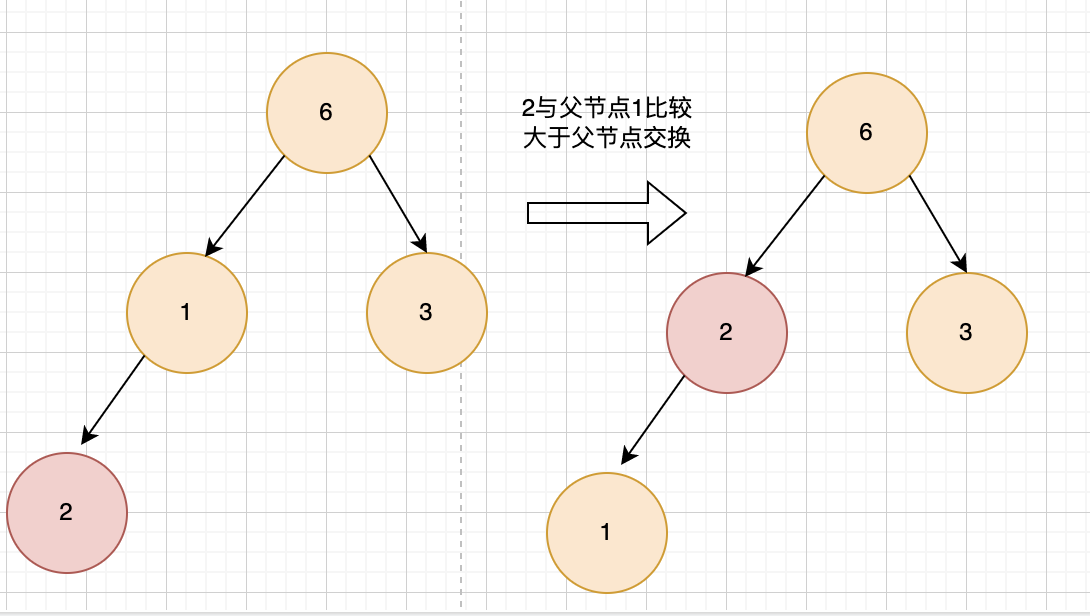
- 第5个数字4,与父节点2比较, 4 > 2,则与父节点交换,此时,4 来到原来2的位置,4继续与父节点6比较,不大于6,暂停,堆化,此时heapSize=5;
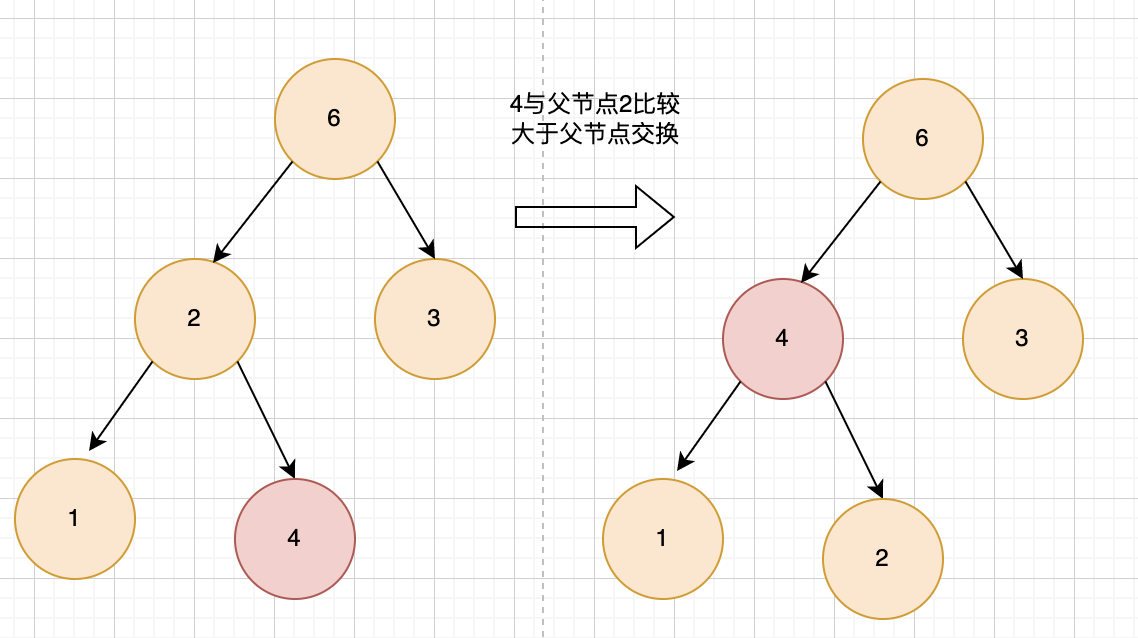
进来一个数字,需要进行一次堆化操作的过程叫做heapInsert过程,即:循环与父节点比较,当大雨父节点时交换,否则停止。
堆化之后,最大值即在跟节点位置,此时最大值已确定。
如何找出其他最大值呢?
跟节点最大值与最后一个节点交换,即最后一个数字已确定为最大值,无需再次进行处理。所以 heapSize - 1, 只需将剩余的元素节点重新堆化(heapify过程)。堆化之后最大值与最后一个元素交换,重复操作。
重要过程
进来一个数字,如何进行heapInsert?
循环进行当前节点元素值与父节点元素比较,大于父节点,则交换位置,直到不满足条件时停止。
代码实现:
1 | func heapInsert(arr []int, index int) { |
跟节点与最后一个节点交换之后,如何叫剩余节点堆化?
- 从跟,如2位置开始,此节点是否有左孩子节点
- 存在左孩子节点4,比较左孩子索引号是否小于heapSize,小于堆化元素则进行下一步。
- 判断父节点2是否有右孩子节点,有孩子节点满足heapSize。
- 找出2位置的左右孩子节点的最大值,与父节点4,进行比较,大于4,则交换,否则,不交换。
- 循环处理,直到剩余节点全部堆化。
代码实现:
1 | func heapify(arr []int, index, heapSize int) { |
如何进行heapSort排序?
代码实现:
1 | func heapSort(arr []int) []int { |
示例
1 | func main() { |
复杂度
时间复杂度: O(NlogN)
空间复杂度,未额外申请空间:O(1)
拓展
- 优先级队列结构,就是堆结构。